
Įxplain how to implement two stacks in one array A in such a way that neither stack overflows unless the total number of elements in both stacks together is n. Using Figure 11.1 as a model, illustrate the result of each of the operations PUSH( S, 4), PUSH( S, 1), PUSH( S, 3), POP( S), PUSH( S, 8), and POP( S) on an initially empty stack S stored in array S.
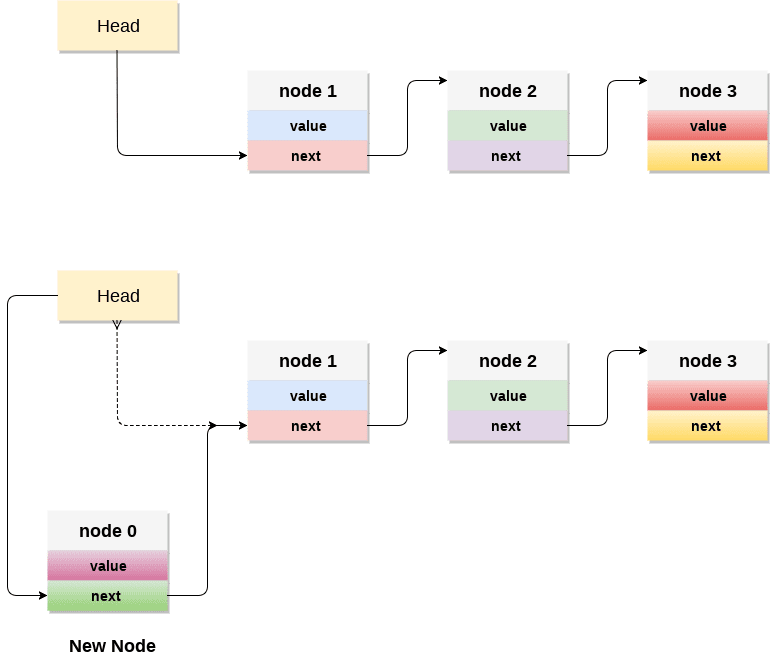
#Linked list stack picture code
(Exercise 11.1-4 asks you to supply code that checks for these two error conditions.)įigure 11.2 shows the effects of the ENQUEUE and DEQUEUE operations. In our procedures ENQUEUE and DEQUEUE, the error checking for underflow and overflow has been omitted. When head = tail + 1, the queue is full, and an attempt to enqueue an element causes the queue to overflow. When the queue is empty, an attempt to dequeue an element causes the queue to underflow. , tail - 1, where we "wrap around" in the sense that location 1 immediately follows location n in a circular order. The elements in the queue are in locations head, head + 1. The attribute tail indexes the next location at which a newly arriving element will be inserted into the queue. The queue has an attribute head that indexes, or points to, its head. The new head has key 6.įigure 11.2 shows one way to implement a queue of at most n - 1 elements using an array Q.

(c) The configuration of the queue after the call DEQUEUE (Q) returns the key value 15 formerly at the head of the queue. (b) The configuration of the queue after the calls ENQUEUE (Q, 17), ENQUEUE (Q, 3), and ENQUEUE (Q, 5). (a) The queue has 5 elements, in locations Q. Queue elements appear only in the lightly shaded positions. (Fortunately, we don't have to worry about computational elements cutting into line.)įigure 11.2 A queue implemented using an array Q. The element dequeued is always the one at the head of the queue, like the student at the head of the line who has waited the longest. When an element is enqueued, it takes its place at the tail of the queue, 1ike a newly arriving student takes a place at the end of the line. The FIFO property of a queue causes it to operate like a line of people in the registrar's office. We call the INSERT operation on a queue ENQUEUE, and we call the D ELETE operation DEQUEUE like the stack operation POP, DEQUEUE takes no element argument. Each of the three stack operations takes O (1) time. The stack operations can each be implemented with a few lines of code.įigure 11.1 shows the effects of the modifying operations PUSH and POP. Although element 3 still appears in the array, it is no longer in the stack the top is element 17. (c) Stack S after the call POP (S) has returned the element 3, which is the one most recently pushed. (b) Stack S after the calls PUSH (S, 17) and PUSH (S, 3). Stack elements appear only in the lightly shaded positions. (In our pseudocode implementation, we don't worry about stack overflow.)įigure 11.1 An array implementation of a stack S. If an empty stack is popped, we say the stack underflows, which is normally an error. The stack can be tested for emptiness by the query operation STACK- EMPTY. When top = 0, the stack contains no elements and is empty. The stack consists of elements S], where S is the element at the bottom of the stack and S] is the element at the top. The array has an attribute top that indexes the most recently inserted element. The order in which plates are popped from the stack is the reverse of the order in which they were pushed onto the stack, since only the top plate is accessible.Īs shown in Figure 11.1, we can implement a stack of at most n elements with an array S. These names are allusions to physical stacks, such as the spring-loaded stacks of plates used in cafeterias. The INSERT operation on a stack is often called PUSH, and the DELETE operation, which does not take an element argument, is often called POP. In this section we show how to use a simple array to implement each. There are several efficient ways to implement stacks and queues on a computer. Similarly, in a queue, the element deleted is always the one that has been in the set for the longest time: the queue implements a first-in, first-out, or FIFO, policy. In a stack, the element deleted from the set is the one most recently inserted: the stack implements a last-in, first-out, or LIFO, policy. Stacks and queues are dynamic sets in which the element removed from the set by the DELETE operation is prespecified. We also discuss a method by which objects and pointers can be synthesized from arrays. Although many complex data structures can be fashioned using pointers, we present only the rudimentary ones: stacks, queues, linked lists, and rooted trees. In this chapter, we examine the representation of dynamic sets by simple data structures that use pointers. Intro to Algorithms: CHAPTER 11: ELEMENTARY DATA STRUCTURES CHAPTER 11: ELEMENTARY DATA STRUCTURES


 0 kommentar(er)
0 kommentar(er)
